
Optymalizacja logistyki dostaw na przykładzie wybranego przedsiębiorstwa
METODA Ε-CONSTRAINTS I PRZEGLĄDU FRONTU PARETO W ZASTOSOWANIU DO ROZWIĄZYWANIA PROBLEMU OPTYMALIZACJI SYSTEMU LOGISTYCZNEGO
WSTĘP
Pojęcie „logistyka” na przestrzeni wielu lat zyskało szereg znaczeń. Jednak według wielu źródeł stanowi koncepcję zarządzania przepływami materiałów, wyrobów gotowych, informacji i ludzi [5, 6, 7, 8]. Ukształtował się również podział logistyki ze względu na obszary zainteresowań. Za najbardziej popularne i obecnie wykorzystywane można wyszczególnić: logistykę zaopatrzenia, produkcji, dystrybucji, transportu, marketingu, odzysku i miejską.
W dobie dzisiejszego rynku globalnego, pojedyncze firmy przestają konkurować ze sobą jako niezależne przedsiębiorstwa z unikalnymi markami, ale jako mniejsze części złożonych struktur łańcuchów dostaw. Ostateczny sukces firmy zależy więc od jej zdolności do integrowania się i koordynowania skomplikowanej sieci relacji biznesowych z pozostałymi partnerami w łańcuchu dostaw [16]. Każde przedsiębiorstwo cechuje się bowiem unikalnym profilem działalności (np. wydobywczej, przetwórczej, produkcyjnej, transportowej, handlowej, marketingowej etc.) stanowiąc indywidualne ogniwo, którego obecność umożliwia funkcjonowanie takiego łańcucha, tworząc spójną całość.
Zintegrowany łańcuch dostaw
Wiele źródeł nazywa to zintegrowanym łańcuchem dostaw, który synchronizuje ze sobą szereg, wzajemnie zależnych procesów, takich jak [8]: pozyskiwanie materiałów i surowców, przetworzenie materiałów i surowców na półwyroby/wyroby gotowe, dodanie wartości do półwyrobów/wyrobów gotowych, dystrybucja i promocja półwyrobów/wyrobów gotowych do klientów, wymiana informacji między różnymi członkami łańcucha dostaw, tj.: (dostawcami, przewoźnikami, detalistami, hurtownikami). Wg M. Christopher’a [6] łańcuch dostaw to sieć organizacji zaangażowanych poprzez powiązania z dostawcami i odbiorcami w różne procesy i działania, które tworzą wartość w postaci produktów i usług dostarczonych konsumentom.
Biorąc pod uwagę przepływy między różnymi obszarami przedsiębiorstwa, to podmiot będący obiektem rozważań niniejszej pracy znajduje się w centrum ŁD. Firma pozyskuje materiały i komponenty, przetwarza je na wyroby gotowe lub półwyroby, a następnie rozsyła do klientów. Oznacza to, że podmiot taki posiada swój „wewnętrzny łańcuch dostaw”, w którym wyróżnić można logistykę zaopatrzenia, produkcji oraz dystrybucji (Rys. 1).
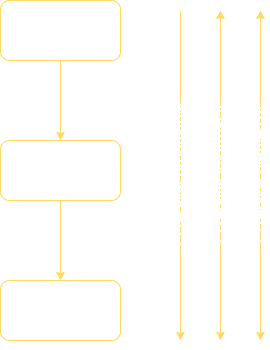
Rys. 1. Ideowy diagram przepływów między różnymi obszarami przedsiębiorstwa [18]
Na każdym etapie łańcucha dostaw jest szereg problemów decyzyjnych o różnorodnym stopniu złożoności, mający charakter operacyjny, taktyczny czy też strategiczny. Powyższe problemy cechują koszty logistyczne (koszty magazynowania, transportu, zamrożonego kapitału), czasy transportu (zarówno materiałów od dostawców jak i wyrobów gotowych do klientów), pracochłonność związana z zarządzaniem materiałami (sporządzanie dokumentacji, manipulacje magazynowe, ocena dostawców, etc.).
OPTYMALIZACJA DOSTAW W SYSTEMACH LOGISTYCZNYCH – PRZEGLĄD WYBRANYCH PODEJŚĆ
W literaturze przedmiotu istnieje wiele badań związanych z optymalizacją systemów dostaw. I tak przykładowo C. Chern i S. Hsieh [4]zaproponowali wielokryterialny model liniowy w celu rozwiązania problemów planowania głównego dla określonego z góry sieci łańcucha dostaw, gdzie zmienna decyzyjną była ilość produkowanego wyrobu gotowego. W modelu uwzględnili takie kryteria, jak: minimalizacja kar z tytułu opóźnień dostaw, minimalizacja wykorzystania przepustowości outsourcingu oraz minimalizacja kosztów produkcyjnych, transportu i magazynowania. Przy konstrukcji modelu wzięto pod uwagę występujące ograniczenia wynikające np. z popytu, jak również pojemności środków transportu i magazynowania.
Podejście Y Chen’a
Z kolei podejście Y Chen’a i in. [3] uwzględnia jedynie dwa kryteria oceny systemu dostaw: minimalizacja łącznych kosztów produkcyjnych oraz transportu i minimalizacja wartości zamówień. W tym przykładzie autorzy uwzględnili nieliniowość problemu. Poza tym także inna była zmienna decyzyjna, tj. wybór określonego dostawcy.
Podejście M. Bassett’a i L. Gardner’a
Znacznie wyższy poziom decyzyjny, bo strategiczny uwzględnia rozwiązanie M. Bassett’a i L. Gardner’a[1], w którym optymalizowana jest struktura globalna łańcucha dostaw dla Dow AgroSciences. Autorzy model oparli o liniowe programowanie całkowitoliczbowe, w którym równolegle optymalizowano projekt sieci łańcucha dostaw oraz miesięczny plan produkcyjny i harmonogram dostaw. Za funkcję kryterialną przyjęto maksymalizację zysków.
Podejście S. Gupta, M. Vanajkumari i C. Sriskandarajah
Natomiast S. Gupta, M. Vanajakumari i C. Sriskandarajah [12] problem optymalizacji systemów dostaw sformułowali jako zagadnienie ustalania harmonogramu dystrybucji, w którym minimalizowano koszty magazynowania dystrybutora, uwzględniając ograniczenia wynikające z produkcji. Innymi słowy problem polegał na rozstrzygnięciu konfliktu między planem produkcyjnym zakładu a harmonogramem prowadzenia wysyłek dystrybutora do swoich klientów i znalezieniu rozwiązania kompromisowego dla obu uczestników łańcucha dostaw.
Podejście M. Grajek i P. Zmuda-Trzebiatowski
W odniesieniu do wyrobów alkoholowych optymalizację systemu dostaw przeprowadził M. Grajek i P. Zmuda-Trzebiatowski [11] oraz M Grajek i in. [10]. Z uwagi na specyfikę ładunku (towary akcyzowe) autorzy zaproponowali tworzenie harmonogramu dostaw od wielu dostawców do jednego odbiorcy. Problem rozpatrywali pod kątem dwóch minimalizowanych kryteriów tj. rozproszenia rozładunków u odbiorcy i rozproszenia załadunków u dostawców. Założono przy tym, że dostawy odbywały się pełnymi pojazdami, a dostawcy zapatrujący odbiorcę będą unikalni.
Podejście C. Chern i S. Hsieh
Podobną zmienną decyzyjną co C. Chern i S. Hsieh [4] zaproponowali w optymalizacji systemu dostaw H. ElMaraghy i R. Majety [9]. Przy czym podejście to polegało na porównaniu dwóch liniowych modeli tego samego łańcucha dostaw. Pierwszy model optymalizowano pod kątem jakości wyprodukowanych wyrobów, a w drugim uwzględniono jeszcze czas dostaw. Przeprowadzone eksperymenty obliczeniowe pozwoliły na dostosowywanie popytu na różne materiały na poszczególnych etapach łańcucha dostaw i rozdział zapotrzebowana na kilku dostawców.
Jak można zauważyć, występujące podejścia są zarówno jednokryterialne, jak i wielokryterialne. Modele są zarówno liniowe, jak i nieliniowe. Oprócz tego zaobserwować można różną metodykę poszukiwania rozwiązań optymalnych, np. metody dokładne, heurystyczne algorytmy wielokryterialne, algorytmy genetyczne, metody rankingowe, czy też interaktywne metody wielokryterialne.
OPTYMALIZACJA DOSTAW W SYSTEMIE LOGISTYCZNYM PRZEDSIĘBIORSTWA
Definicja problemu decyzyjnego, uczestnicy procesu decyzyjnego
Problem decyzyjny zdefiniowano jako ustalenie momentu dostaw określonego materiału wchodzącego w skład wcześniej zdefiniowanego wyrobu gotowego, który został zamówiony przez znanego klienta. Poszczególne materiały dostarczane są przez znanych z góry różnych producentów zlokalizowanych na różnych kontynentach (rys. 2). Mogą być one transportowane przez firmy zewnętrzne:
– drogą lotniczą,
– drogą lądową (głównie transport drogowy).
Oprócz tego rozważany jest transport także przez producenta.
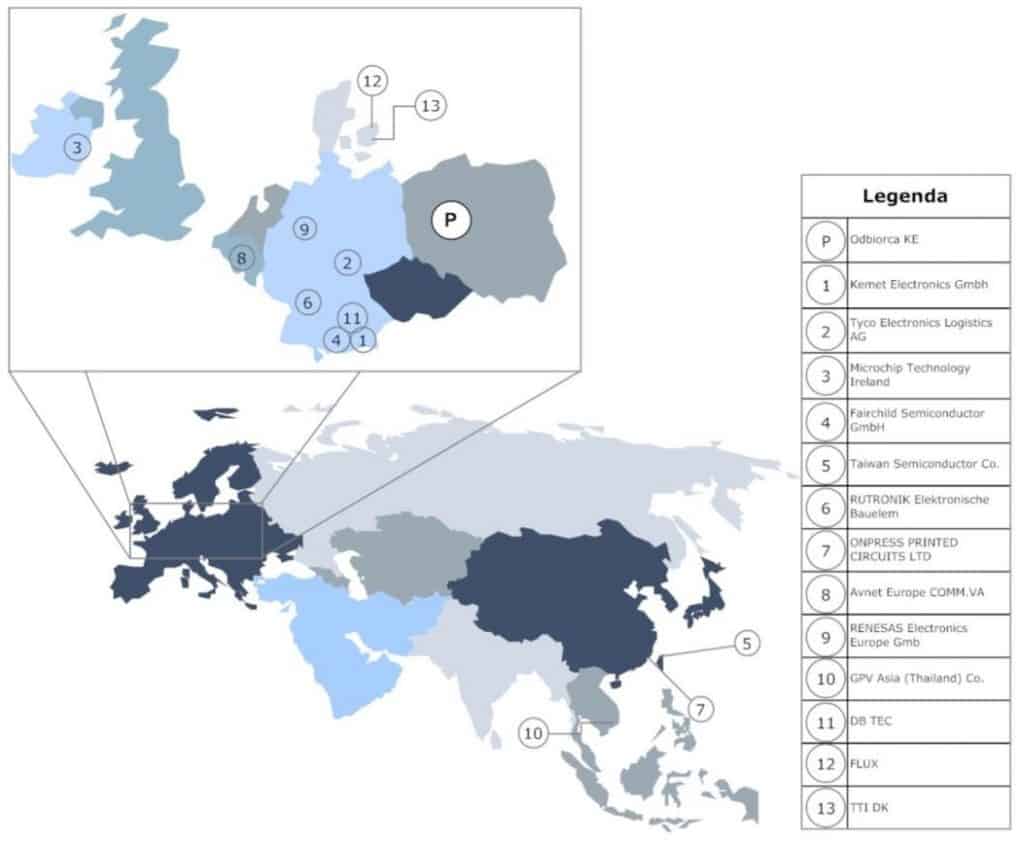
Rys. 2. Rozmieszczenie wybranych dostawców na świecie
Na podstawie analizy sytuacji decyzyjnej rozważane zagadnienie można z punktu widzenia różnych kryteriów zaliczyć do problemów wyboru, strategicznych, deterministycznych, pośrednio określanych z góry oraz statycznych.
Interesariusze
W rozważanym przykładzie optymalizacji problemu zidentyfikowano 4 uczestników procesu decyzyjnego: dział zaopatrzenia, dział magazynowania, dział marketingu i sprzedaży oraz strefa zarządu, których różnicują oczekiwania (tab. 1.).
Zarządzanie dostawami materiałów i surowców wiąże się dużą liczbą podejmowanych decyzji. Każdy uczestnik (dział) procesu charakteryzuje się własnymi preferencjami oraz posiada informacje potrzebne pozostałym. Najczęściej wymienione w tab. 1. oczekiwania tworzą pewna całość ukierunkowana na jeden cel, tj. dobro klienta. Niemniej jednak każdy dział w różny sposób podchodzi do tego zagadnienia i operuje innymi informacjami, które przenikają poniekąd przez pozostałe działy. Może to zdaniem autorów artykułu skutkować wewnętrznym konfliktem interesów. Stad też niezwykle cennym jest ocena stopnia wpływu poszczególnych elementów na osiąganie wspólnego celu.
Tab. 1 Oczekiwania uczestników procesu decyzyjnego
| Dział Zaopatrzenia | Dział Magazynowania | Dział Marketingu i Sprzedaży | Strefa Zarządu |
|---|---|---|---|
| Zmniejszenie kosztów dostaw towarów | Zmniejszenie kosztów magazynowania | Ustalenie stabilnego i znanego popytu klienta | Zmniejszenie kosztów zamrożonego kapitału |
| Redukcja czasu dostaw materiałów | Redukcja czasu składowania materiałów | Wydłużenie terminów realizacji zamówień wyrobu gotowego | Zwiększenie pracochłonności |
| Zmniejszenie czasów realizacji zamówień | Równomierne obciążenie miejsc magazynowych | Posiadanie bieżących prognoz dotyczących sprzedaży | Utrzymanie zgodnych relacji biznesowych |
| Uzyskanie długich terminów płatności | Ujednolicenie jednostek ładunkowych i nośników | Zwiększenie poziomu jakości obsługi klientów | Zwiększenie wydajności produkcyjnej |
Model matematyczny
Założenia ogólne
Model matematyczny poruszanego w artykule problemu decyzyjnego sformułowano jako wielokryterialne zadanie optymalizacji kombinatorycznej. Przyjęto w nim następujące założenia:
– Znana jest skończona liczba materiałów danego wyrobu gotowego.
– Materiały z którego wykonywane są wyroby gotowe są wykorzystywane do produkcji tylko
jednego wyrobu.
– Znany jest maksymalny, stały poziom zapasów poszczególnych materiałów, który jest
równomiernie rozłożony w zakładanym przedziale czasowym.
– Całkowity okres rozważań wynosi 52 tygodnie (w przybliżeniu 1 rok).
– Popyt na dany wyrób gotowy jest znany i niezmienny w czasie.
– W ciągu 4 tygodni musi nastąpić 1 dostawa materiałów.
Zmienne decyzyjne
W przyjętym modelu matematycznym problemu decyzyjnego założono istnienie dwóch rodzajów zmiennych decyzyjnych:
- – podstawowej – , którą zdefiniowano jako moment realizacji dostaw materiałur w określonym tygodniu t, znanego z góry horyzontu czasowego, co zapisano matematycznie:
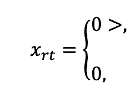 | jeżeli dostawa materiału r zostanie zrealizowana w tygodniu t,w przeciwnym wypadku dla, r = 1, …, R; t = 1, …, T | (1) |
- – pomocniczej (zależnej) – , określającej częstotliwośćz jaką mają być realizowane poszczególne dostawy, co zapisano matematycznie:
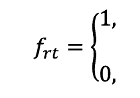 | jeżeli dostawa materiału r zostanie zrealizowana w tygodniu t,w przeciwnym wypadku dla, r = 1, …, R; t = 1, …, T | (2) |
Przy tak założonych zmiennych decyzyjnych ich liczba znacząco wzrasta, w zależności od
przyjętej liczby przedziałów czasowych (t) oraz liczby rozważanych materiałów (r).
Kryteria
Proponowany model matematyczny problemu decyzyjnego uwzględnia zestaw pięciu kryteriów istotnych z punktu widzenia rozważanego problemu decyzyjnego. Pierwsze z nich – koszty magazynowania (Kmag ) zdefiniowano następująco:
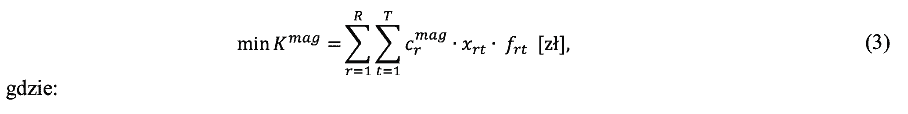
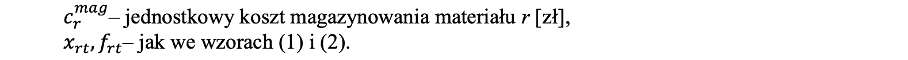
Drugie z kryteriów – koszty transportu ( Ktrans)zaproponowano tak, by możliwe było uwzględnienie wielkości poszczególnych, znanych z góry elementów r:
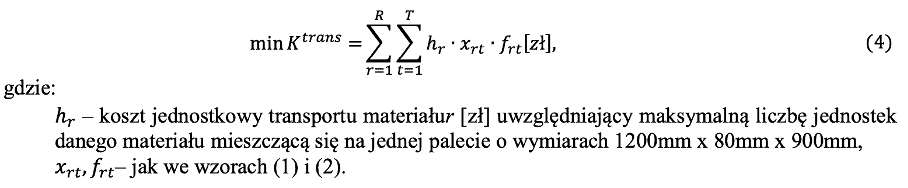
Ostatnie z kryteriów kosztowych – koszty zapasów w drodze (Kzwd) pozwala odnieść się do zamrożonych aktywów w srodze. Kryterium to jest minimalizowane i przyjmuje postać:

Czwarte z kryteriów – czas transportu (Ttrans ) uwzględnia czas potrzebny na przewiezienie poszczególnych materiałów od dostawcy do odbiorcy. Pozwala to na wcześniejsze zorganizowanie zarówno procesów produkcyjnych, jak i magazynowych (przygotowanie przyjęcia zamówienia). Co więcej posiadając całkowity czas transportu potrzebny na funkcjonowanie systemu dostaw można określić średnie, miesięczne czasy przewozu, a co za tym idzie odpowiednio rozłożyć zadania i czynności w czasie. Mając na uwadze powyższe kryterium to ma postać:
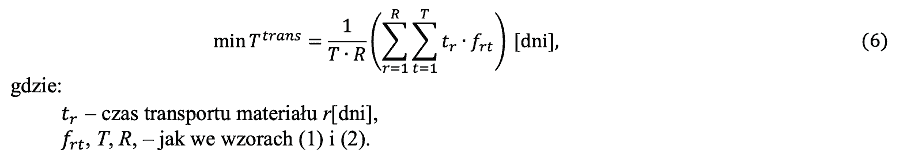
W ostatnim kryterium branym pod uwagę w modelu jest wydajność w jednostce czasuprzy pracach personelu magazynowego – Eprac. Istotą tego kryterium jest odpowiednie dostosowanie harmonogramu dostaw, aby równomiernie rozłożyć zamawiane materiały. Przyczyną jest czasochłonna obsługa komponentów tj. przyjęcie zamówienia, rozpakowanie towaru, rozłożenie na miejsca składowe. Mając na uwadze powyższe kryterium to zapisano:
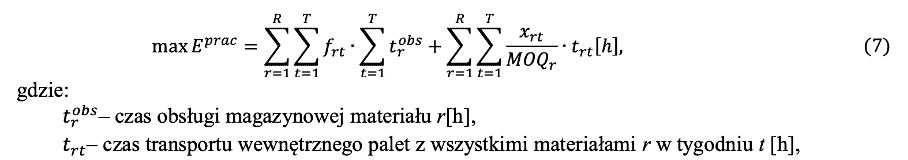

Na podstawie analizy sytuacji decyzyjnej zaobserwowano, że poszczególne kryteria posiadają różną istotność wśród potencjalnych interwenientów – poszczególnych zidentyfikowanych działów przedsiębiorstwa. Średnio najwyżej w rankingu są kryteria: koszty transportu i koszty zapasów w drodze. Na kolejnym miejscu: koszty magazynowania oraz czas transportu. Najniżej w rankingu jest kryterium wydajności, które wg indywidulanych rankingów poszczególnych działów w większości przypadków plasuje się na 4-5 miejscu (jedynie dział magazynowania wskazał, że kryterium to powinno być na 2 miejscu.
Ograniczenia
W modelu matematycznym uwzględniono następujący zestaw ograniczeń:
– Łączna wielkość dostaw poszczególnych materiałów musi spełniać warunek zapotrzebowania w stopniu równym lub większym oczekiwaniom.
– Maksymalna wielkość materiałów w ciągu roku (okresu T) nie może przewyższać 125% antycypowanego popytu.
– Tygodniowa wielkość dostawy materiału r nie może przekraczać maksymalnego, dostępnego miejsca składowego dla tego materiału; wielkość miejsca składowego równa jest miesięcznemu zapotrzebowaniu na dany materiał.
– Suma dostaw materiału r w miesiącu n nie może przekraczać miesięcznego zużycia tego materiału.
– W miesiącu musi nastąpić co najmniej jedna dostawa materiału r.
Procedura rozwiązywania problemu
W procedurze rozwiązywania problemu wykorzystano zbiór danych wejściowych znajdujących się w posiadaniu przedsiębiorstwa ABC3. Oprócz tego wykorzystano także wiedzę i doświadczenie pracowników z poszczególnych działów (interwenientów). Zakres zebranych danych obejmował zbiór kluczowych elementów systemu dostaw:
– specyfikacja materiałowa wyrobu gotowego,
– baza dostawców materiałów,
– baza przewoźników materiałów,
– popyt na wyrób gotowy,
– dodatkowe informacje stałe takie jak rodzaj jednostki ładunkowej, nośnik materiałów, czasy
realizacji zamówień, czasy transportu.
Przy wykonywaniu eksperymentów obliczeniowych wykorzystano często stosowaną, procedurę dwuetapową [10, 11,15] tj.:
– generowanie zbioru rozwiązań – etap I,
– przegląd i wybór rozwiązania satysfakcjonującego – etap II.
W pierwszym z tych etapów autorzy zastosowali metodę dodatkowych ograniczeń – ε-constraints [17], natomiast w drugim metodę przeglądu frontu Pareto. Pierwsza z nich należy (ε-constraints) do grupy metod dokładnych, której początki sięgają lat 70’ ubiegłego wieku [13]. Pozwala wygenerować wyniki dla poszczególnych celów przy uwzględnieniu dodatkowych ograniczeń, którymi są pozostałe kryteria. Decydent wybiera to kryterium (bądź kryteria) względem, którego chciałby wygenerować rozwiązania. Dzięki uzyskanej informacji jaką jest przestrzeń (zakres) przypuszczalnych rozwiązań z uwagi na dodatkowe ograniczenia decydent będzie w stanie ustalić swego rodzaju „krok”, co który będzie analizował (generował) kolejne rozwiązania. Do generowania rozwiązań wykorzystano narzędzie Evolver z rodziny aplikacji komputerowych Palisade Decision Toolset stanowiące rozszerzenie do programu Excel pakietu MS Office. Narzędzie to bazuje na algorytmach ewolucyjnych, stąd też dedykowane jest do rozwiązywania problemów o charakterze nieliniowym.
Pareto Front Viewer
Z kolei druga z metod polega na określonym przeglądzie rozwiązań tzw. pareto-optymalnych, które zgodnie z metodyką wielokryterialnego wspomagania decyzji winny być brane przy wyborze wariantu kompromisowego. W etapie tym wykorzystanoprogram PFV (ang. Pareto Front Viewer) zaproponowane przez G. Kamenev’a i A. Lotov’a [2]. Podobnie jak LBS [2] czy też ClaferMooVisualizer [14] narzędzie to zapewnia decydentowi interaktywną wizualizację rozwiązań problemów wielokryterialnych. Mechanizm działania narzędzia ma charakter empiryczny (tzw. a posteriori) prowadzący do wyszukiwania rozwiązań kompromisowych. W przeciwieństwie do klasycznych metod rozwiązywania problemów decyzyjnych, PFV nie wymaga od decydenta definiowania preferencji w procesie uzyskiwania rozwiązań dopuszczalnych lecz pomaga je określić. Interakcja użytkownika następuje dopiero po aproksymacji procesu czyli odnalezieniu rozwiązań ze zbioru kryteriów znajdujących się najbliżej frontu Pareto za pomocą techniki interaktywnych map decyzyjnych (ang. Interactive Decision Maps – IDM). Wizualizacja wyników w narzędziu PFV jest oparta o zmodyfikowany w IDM wykres Edgheworth (tzw. wykres Edgeworth-Pareto Hull).
Generowanie rozwiązań
Początkowa faza generowania rozwiązań opierała się na poszukiwaniu rozwiązań optymalnych z punktu widzenia każdego z kryteriów. Pozwoliło to na określenie tzw. punktu idealnego (ang. ideal point) oraz punktu najgorszego (ang. nadir point) – tab. 2.
Dzięki wyznaczeniu współrzędnych punktów idealnego i nadir dla poszczególnych kryteriów decydent był w stanie ocenić rozpiętość możliwych rozwiązań i określić minimalne i maksymalne wielkości.
Tab. 2. Wartości poszczególnych kryteriów dla początkowej fazy generowania rozwiązań – punkt idealny i punkt najgorszy.
| Nazwa punktu | Kryterium | ||||
| Koszty magazynowania K mag [zł] | Koszty transportu Ktrans [zł] | Koszty zapasów w drodze Kzwd [zł] | Czas transportu Trans [dni] | Wydajność Eprac [h] | |
| Idealny | 25 742 | 300 002 | 11 335 | 3,19 | 14,83 |
| Najgorszy | 19 998 | 355 619 | 12 766 | 2,32 | 8,15 |
Zgodnie z metodyką ε-constraints ustalono krok zmian dla dodatkowego ograniczenia. Oznaczało to stałą wartość ε, o którą musi być pomniejszona wielkość kryterium ograniczającego, aby wygenerować kolejny wynik rozwiązania. Cała procedura wykonana została przy wykorzystaniu dodatku Evolver, a dodatkowe warunki ograniczające wprowadzono w podobny sposób jak podczas optymalizacji jednokryterialnej. Proces został powtórzony dla wszystkich pięciu celów, co w wyniku dało listę 93 różnych ocen rozwiązań. Wygenerowany zbiór ocen rozwiązań charakteryzuje się następującymi parametrami:
| średnia wartość kryterium kosztów magazynowania [K mag] | 22 351 zł |
| średnia wartość kryterium kosztów transportu [K trans] | 323 157 zł |
| średnia wartość kryterium kosztów zapasów w drodze [K zwd] | 12 311 zł |
| średnia wartość kryterium czasu transportu [K trans] | 2,69 dnia |
| średnia wartość kryterium wydajności [E prac] | 11,69 h |
Przegląd rozwiązań i wybór kompromisowego
W etapie tym w pierwszej kolejności dokonano analizy rozwiązań zmieniając płaszczyzny rzutowania na poszczególne kryteria. Pozwoliło to na sprawdzenie spektrum zmienności wygenerowanych w etapie I rozwiązań. Niektóre iteracje zaprezentowano na rys. 3. Przykładowo na grafie – rys. 3a zdefiniowano na osi x kryterium kosztów magazynowania, na osi y kryterium kosztów transportu, a płaszczyzną rzutowania z było kryterium wydajności. Finalnie, zdecydowano się na opcję, w której poszczególne osie oznaczają: x – wydajność, y – koszty zapasów w drodze, z – koszty magazynowania. Wykres Edgeworth-Pareto Hull dla przyjętego rzutowania przedstawiono na rysunku 3d.
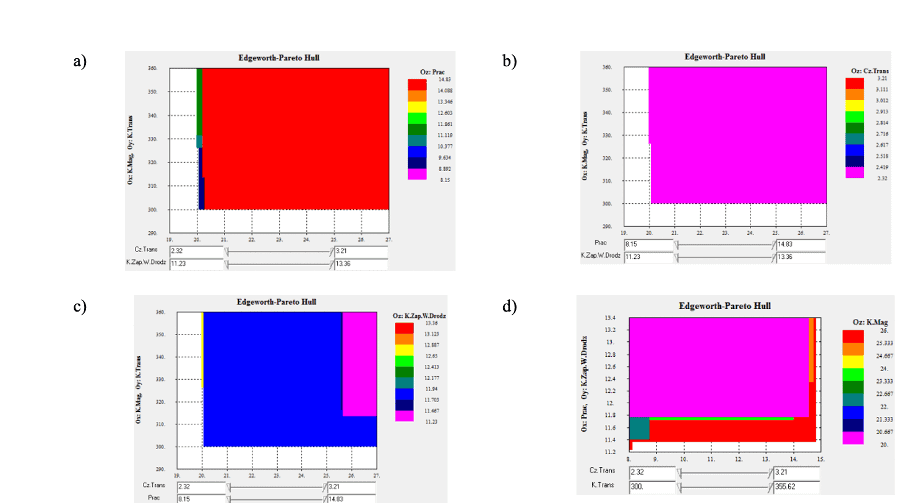
Rys. 3. Wykres Edgeworth-Pareto Hull dla różnych płaszczyzn rzutowania w programie PFV: a) iteracja 1, b) iteracja 2, c) iteracja 3, d) iteracja 4
Następnie na podstawie poziomu aspiracji uczestników procesu decyzyjnego określono wartości poszczególnych kryteriów, które mają spełniać oczekiwania lub być najbliżej idealnego rozwiązania w stosunku do preferencji (tab. 3)
Tab. 3. Oczekiwane wartości poszczególnych kryteriów przez uczestników procesu decyzyjnego
| Nazwa kryterium | Dział zaopatrzenia | Dział magazynowania | Dział marketingu | Sfera zarządu |
|---|---|---|---|---|
| Koszty magazynowania [tys. zł] | 25 | 15 | 26 | 21 |
| Koszty transportu [tys. zł] | 300 | 350 | 300 | 330 |
| Koszty zapasów w drodze [tys. zł] | 11 | 13 | 11, 35 | 10 |
| Czas transportu [dni] | 2,25 | 2,50 | 2,75 | 3,00 |
| Wydajność [h] | 14 | 8 | 11 | 13 |
Finalnie w wyniku dyskusji z przedstawicielami poszczególnych działów, ustalono punkt referencyjny, dla którego wartość poszczególnych kryteriów wyniosły:
- Koszty magazynowania – 21 750 zł
- Koszty transportu – 320 000 zł
- Koszy zapasów w drodze – 11 460 zł
- Czas transportu – 2,63 dnia
- Wydajność – 11,46 h
W wyniku analizy wykresu Edgeworth-Pareto Hull stwierdzono, że rozwiązanie kompromisowe to wariant 42, w którym wartości kryteriów są najbliżej oczekiwanym i wynoszą odpowiednio:
- Koszty magazynowania – 22 070 zł
- Koszty transportu – 328 110 zł
- Koszy zapasów w drodze – 11 400 zł
- Czas transportu – 2,68 dnia
- Wydajność – 11,40 h
Jak można zaobserwować, że w przypadku trzech kryteriów wartości rozwiązania kompromisowego są nieznacznie gorsze w porównaniu z oczekiwanymi (różnica na poziomie 2-3%). Największą różnicą cechuje się niestety kryterium wydajności, gdyż uzyskany wynik jest gorszy o ponad 30%. Oznacza to, że średnia liczba tygodniowych prac magazynowych wzrosła prawie o 3h. Jeśli chodzi o ostatnie kryterium tj. kryterium zapasów w drodze to uzyskane rozwiązanie spełnia wymagania. Co więcej jest o 0,5% lepsze niż oczekiwane, a to oznacza, że firma zamraża o 0,5% mniej kosztów rocznie.
WNIOSKI
Jak można zauważyć problem optymalizacji systemu logistycznego jest zagadnieniem złożonym. W przypadku rozważanego przypadku – optymalizacji dostaw wymaga on uwzględnienia opinii wielu uczestników procesu decyzyjnego. Należy zaznaczyć, że analiza specyfiki funkcjonowania przedsiębiorstwa skutkowała tym, iż konieczne było rozdzielenie kryterium kosztowego na trzy składowe: koszty magazynowania, koszty transportu i koszty zapasów w drodze. Przedstawione podejście potwierdza przydatność stosowanych metod i narzędzi optymalizacji do rozwiązywania problemu dostaw.
Jeżeli powyższy przykład Ciebie zainteresował i chciałbyś podobny projekt zrealizować u Siebie zapraszamy do kontaktu.
BIBLIOGRAFIA
- Bassett M., Gardner L.,Optimizing the design of global supply chain at Dow AgroSciences, Computers and Chemical Engineering 2010, vol. 34, s. 254-265.
- Branke J., Deb K., Miettinen K., Słowiński R. (red.),Multiobjective optimization: interactive and evolutionary approaches. State-of-the-Art Survey series of the Lecture Notes in Computer Science, no. 5252, Springer-Verlag, Berlin 2008.
- Chen Y., Che Z., Chiang T., Chiang C., Che Z.,Modelling and Solving the Collaborative Supply Chain Planning Problems. W: S. Chou, A. Trappey A., Pokojski J., Global Perspective for Competitive Enterprise, Economy and Ecology Proceedings of the 16th ISPE International Conference on Concurrent Engineering.
- Chern C., Hsieh J., A heuristic algorithm of master planning that satisfies multiple objectives.Computers and Operations Research 2007, vol. 34, s. 3491-351.
- Christopher M.,Logistics and Supply Chain Management. Creating Value-Adding Networks, Prentice Hall, 2005.
- Christopher M., Logistyka i zarządzanie łańcuchem dostaw. Strategie obniżki kosztów i poprawy poziomu obsługi.Polskie Centrum Doradztwa Logistycznego, Warszawa 2000.
- Ciesielski M.,Istota logistyki, podstawowe pojęcia. W: Gołembska E. (red.): Kompendium wiedzy o logistyce, Wydawnictwo Naukowe PWN, Warszawa, 2002, s. 44-51.
- Coyle J., Bardi E., Langrey C.,Zarządzanie Logistyczne. Polskie Wydawnictwo Ekonomiczne, Warszawa 2002.
- ElMaraghy H. A., Majety R.,Integrated supply chain design using multi-criteria optimization.International Journal of Advanced Manufacturing Technology 2007, Springer-Verlag London Limited, s. 371-399.
- Grajek M., Kiciński M., Bieńczak M., Żmuda-Trzebiatowski P.,MCDM approach to the excise goods daily delivery scheduling problem. Case study: alcohol products delivery scheduling under Intra-Community Trade regulations. Procedia – Social and Behavioral Sciences 01/2014, 111:751-760.
- Grajek, M., Zmuda-Trzebiatowski P.,A heuristic approach to the daily delivery scheduling problem. case study: alcohol products delivery scheduling within intra-community trade legislation. LogForum 2014, no. 10 (2), s. 163-173.
- Gupta S., Vanajakumari M., Sriskandarajah C.,Sequencing deliveries to minimize inventory holding cost with dominant upstream supply chain partner. Systems Engineering Society of China & Springer-Verlag, vol. 18(2), s. 159-183.
- Haimes Y., Ladson L., Wismer D.,On a bicriterion formulation of the problems of integrated system identification and system optimization. IEEE Transactions on Systems 1971, Man and Cybernetics, vol. 1, s. 296-297.
- Kiciński M., Wielokryterialne harmonogramowanie obsług taboru w przedsiębiorstwie publicznego transportu autobusowego. Rozprawa doktorska. Politechnika Poznańska, Poznań 2012.
- Lambert D., Cooper M.,Issues in supply chain management. Industrial Marketing Management 2000, no. 29, s. 65-83.
- Mavrotas G.,Effective implementation of the ε-constraint method in Multi-Objective Mathematical Programming problems. Applied Mathematics and Computation, Elsevier, 2003, vol. 213, s. 455-465.
- Witort P., Metoda ε-constraints i przeglądu frontu pareto w zastosowaniu do rozwiązywania problemu optymalizacji systemu logistycznego. Praca dyplomowa magisterska nr 13/DzM/Lt/13/14. Politechnika Poznańska, Poznań 2014.






2 komentarze
Pingback:
Windows CMD
Bardzo ciekawy blog, rzeczowy i wyważony. Od dzisiaj zaglądam regularnie i subsbskrybuję kanał RSS. Pozdrowienia 🙂